Surface growth studies


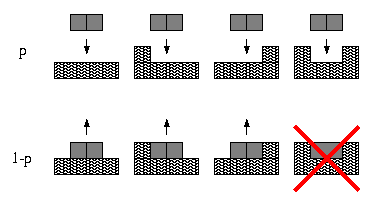
In Ref. [21]  we introduced a model for the growth of an interface by dimer adsorption and desorption. Dimers (composite particles consisting of two atoms) are adsorbed at sites of equal height at rate p and evaporate at rate 1-p. The key feature of our model is that evaporation is allowed only at the edges of terraces. In 1+1 dimensions the dynamic rules are:

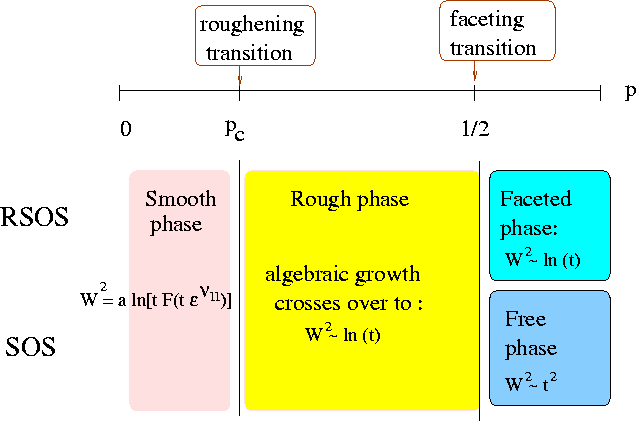
One of the most interesting properties of this model is a roughening transition from a smooth to a rough phase at the critical threshold p=0.3167. The following figure illustrates typical interface morphologies for various values of p:

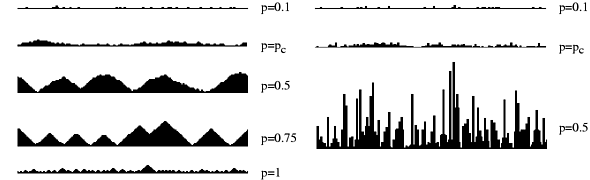
                     Restricted solid on solid (RSOS) version                                Unrestricted solid on solid (SOS) version
 

In the smooth phase, the interface selects spontaneously one height level as the bottom layer of the interface. The roughening transition is related to the so-called parity-conserving universality class (PC) which is represented most prominently by branching-annihilating random walks with two offspring A->3A, 2A->0.   In such a process the particle density vanishes according to a power law with a certain critical exponent

n ~ (p-pc)0.92.

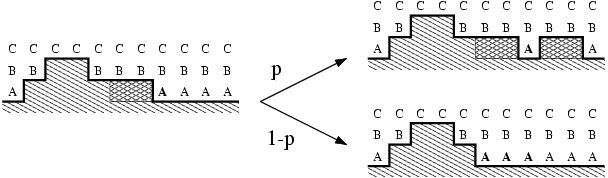
It can be shown that the density of exposed sites at the bottom layer in our model vanishes with the same critical exponent, showing that the roughening transition is closely related to the PC class. In fact, the critical behavior at the first few layers may be explained in terms of unidirectionally coupled PC processes:
 


 
 
 

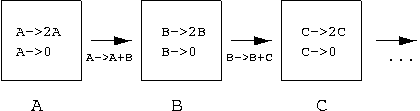
In Ref. [22] we explored the phase structure of several variants (SOS, RSOS,random sequential, parallel update) of this model in the p=(0,1) region and show that all variants display the same type of universal critical behavior at the roughening transition. Besides the roughening transition there is a faceting transition as well at the symmetry point of the model (p=1/2). The scaling properties are insensitive on whether we use parallel or random sequential updates.
 


 
 

If we start the system from random initial distribution of hights h=0,1
the dynamical properties will be different as the consequence of
hard-core interactions. Moreover, a parity conserving polynuclear
growth model is proposed that exhibits the same critical behavior
at the roughening transition point as the dimer model.



 




































For more details see Ref. [52] , Talk at Rathen  , [56]  or talk of IINM-2011 (Bhubaneswar, India) arXiv:1109.2717.

This kind of mapping can be generalized to d-dimensions: the surface deposition/removal corresponds to the migration of directed d-mers of d-dimensional lattice gases. Hence, for example the KPZ behavior can be studied by binary lattice gases effectively [55]  [58]  [60]. In three dimensions we have diffusing triangles with exclusions as shown on the figure below.


Surface pattern formation can be analyzed via mapping onto different lattice gases. See chapter 9 in [66].


Disorder can also be relevant in surface gwowth causing different scaling behavior, usually with slow dynamics [63].


Ageing in nonequilbrium systems, caused by broken time translational symmetry has also been studied in the 2+1 dimensional KPZ model [70],[81] and Logarigthmic Local Scale Invariance is supported [78].

Dec 18 2017