Networks, brain, sociophysics, population dynamics, long-range
interactions
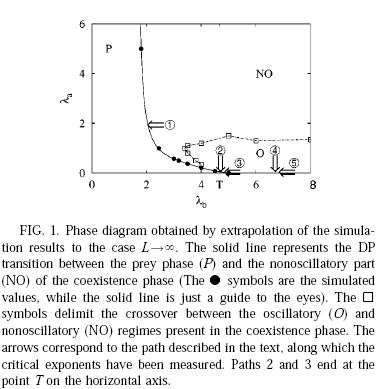 The
application of nonequilibrium statistical physics in various other
branches of sciences, has been flourished in the past decades. The
modeling and tools of physics have opened a new way of analyzing
these complex system. Statistical physics can describe population
dynamics of animals or plants and can
explain extinction or oscillation phenomena observed in nature.
Besides the traditional mathematical approaches based on
differential equations it can take into account fluctuations
observed in predator-prey
models.
The
application of nonequilibrium statistical physics in various other
branches of sciences, has been flourished in the past decades. The
modeling and tools of physics have opened a new way of analyzing
these complex system. Statistical physics can describe population
dynamics of animals or plants and can
explain extinction or oscillation phenomena observed in nature.
Besides the traditional mathematical approaches based on
differential equations it can take into account fluctuations
observed in predator-prey
models.
We
have investigated simple predator-prey models [30]
and for some values of the control parameters we found that the
model exhibits a line of directed percolation like transitions to a
single absorbing state. For other values of the control parameters
one finds a second line of continuous transitions toward an infinite
number of absorbing states, and the corresponding steady-state
exponents are mean-field-like. The critical behavior of the special
bicritical point, where the two transition lines meet, belongs to a
different universality class. A particular strategy for preparing
the initial states used for the dynamical Monte Carlo method is
devised to correctly describe the physics of the system near the
second transition line.
 It
is worth to mention, that our model is closely related to a model
introduced by Drossel and Schwabl to investigate the effect of
immunization in an extension of the simple
forest-fire model.
That three-state model (0 is an empty site, 1 is a tree, and 2 is a
burning tree) differs
from our model in some details: the growth rate of a tree (s
: 0
->1) is p
, independently of
the environment, and a tree is ignited (s
: 1->
2) with rate (1-g
)Q
(n2
), (Q
is the usual
Heaviside function) .
This second process models the immunization of trees against fire.
The third process (s
: 2 ->
0) occurs at rate
1. For nonzero immunity and p>0, Albano showed that a transition
toward a single absorbing state is DP like, while for p=0 (at the
end point of the DP transition line), the transition belongs to the
dynamical percolation universality class, and the absorbing state is
not unique.
It
is worth to mention, that our model is closely related to a model
introduced by Drossel and Schwabl to investigate the effect of
immunization in an extension of the simple
forest-fire model.
That three-state model (0 is an empty site, 1 is a tree, and 2 is a
burning tree) differs
from our model in some details: the growth rate of a tree (s
: 0
->1) is p
, independently of
the environment, and a tree is ignited (s
: 1->
2) with rate (1-g
)Q
(n2
), (Q
is the usual
Heaviside function) .
This second process models the immunization of trees against fire.
The third process (s
: 2 ->
0) occurs at rate
1. For nonzero immunity and p>0, Albano showed that a transition
toward a single absorbing state is DP like, while for p=0 (at the
end point of the DP transition line), the transition belongs to the
dynamical percolation universality class, and the absorbing state is
not unique.
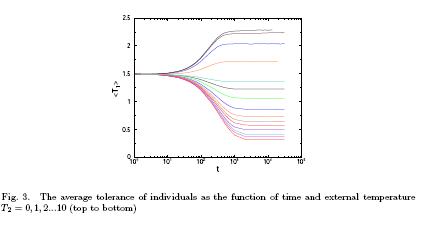 The
problem
of human
segregation
is an important problem of society and politics even in the 21st
century. Social sciences have been investigating the reasons and and
nature of segregation for a long time. Sociologist have introduced
several models, one of them is the Schelling model 2. From physicist
point of view that model is a 3-state voter-type non-equilibrium
model (groups A,B and empty), with spin-exchange dynamics at zero
temperature (T = 0) on a 2-dimensional square lattice. Although the
model describes a segregation by a quench without external reasons,
unwanted frozen states may also occur. As
an application of the knowledge of nonequilibrium models we have also
investigated a social related model as a proposal of Prof. D.
Stauffer.
The
problem
of human
segregation
is an important problem of society and politics even in the 21st
century. Social sciences have been investigating the reasons and and
nature of segregation for a long time. Sociologist have introduced
several models, one of them is the Schelling model 2. From physicist
point of view that model is a 3-state voter-type non-equilibrium
model (groups A,B and empty), with spin-exchange dynamics at zero
temperature (T = 0) on a 2-dimensional square lattice. Although the
model describes a segregation by a quench without external reasons,
unwanted frozen states may also occur. As
an application of the knowledge of nonequilibrium models we have also
investigated a social related model as a proposal of Prof. D.
Stauffer.
A
two-temperature Ising-Schelling model is introduced and studied for
describing human segregation. The self -organized Ising model with
Glauber kinetics simulated by Muller et al. exhibits a phase
transition between segregated and mixed phases mimicking the change
of tolerance (local temperature) of individuals. The effect of
external noise is considered here [50]
as a second temperature to the decision of individuals who
consider change of accommodation.
|
|
|
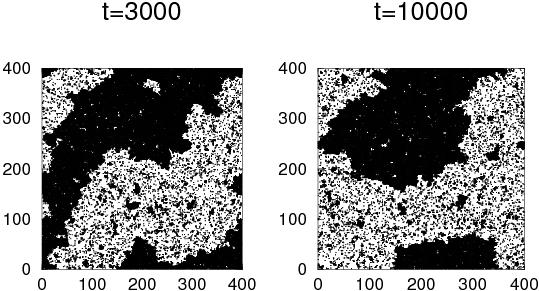
Fig.
2. Clusters survive small external noise in 2d simulations
(numbers on the axes denote lattice location), hence the inclusion
of a small second temperature does not change the composition of
neighbors in the steady state. From ref. G. Ódor,
Self-organizing, two-temperature Ising model describing human
segregation,
arXiv:0710.1496
Int.
J. Mod. Phys C 19 (2008) in 393.
|
Quenched disorder is known to play a relevant
role in dynamical processes and phase transitions.
Effects on the dynamics of complex networks have hardly been studied.
Aimed at filling this gap, we have analyzed the contact process, i.e., the simplest
propagation model, with quenched disorder on complex networks. We found
Griffiths phases and other rare-region effects,
leading generically to anomalously slow (algebraic, logarithmic, . . .) relaxation ,
on Erdos-Renyi networks.
Similar effects are predicted to exist for other topologies with a
finite percolation threshold. More surprisingly, we found that Griffiths
phases can also emerge in the absence of quenched disorder, as a
consequence of topological heterogeneity in networks with finite
topological dimension. These results have a broad spectrum of implications
for propagation phenomena and other dynamical processes on networks
[57],[59],[62],[64],[67],[68],[69],[71],[72],[72],[73].
Even in finite scale-free networks one can
also find Griffiths effects and slow dynamics in extended parameter
regions [64],[74].
Recently we showed numerical evidence for Griffiths phase in modular networks possessing
infinite topological dimensions
[82].
More interstingly it turns out that at criticality or in the Griffiths phase
bursty behavior of agents can emerge as consequence
of quenched network topologies [71].
This has been studied in synthetic brain networks
[73],
and the possibilty of
Griffiths effects
in large human connectome networks
has also been pointed out
[75],
[77],
[79],
[85].
Heterogeneities also play an important role at network synchronization phenomena,
[87], which occur in brain models
[88],
[92], [93],
[94],
[98],
[104],
in power-grids
[83], [86], or in epidemic models
[91].
|
|
|
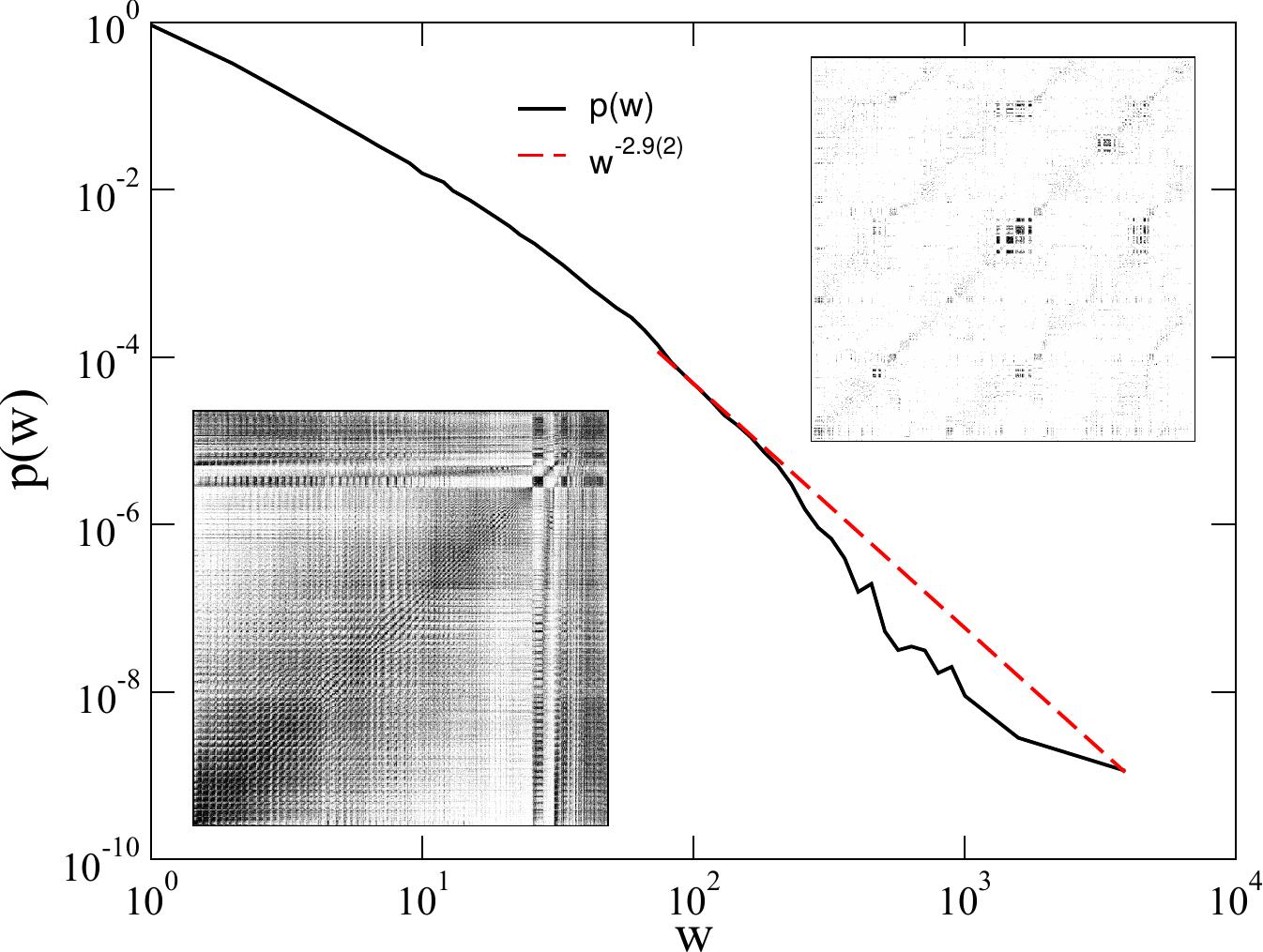
Fig. 4.
Weight distribution of the fruit-fly connectome.
Right inset: adjacency matrix plot of the fruit-fly connectome.
Black/white dots denote connected/unconnected nodes
i (vertical), j (horizontal). Left inset: full adjacency matrix down-sampled with a max pooling kernel of size 10 x 10,
arXiv:0710.1496
|
Avalanche dynamics is not only interesting in
brain models [93],
but also in case of power-grids [[95],
[89] and in fiber bundle models
[100], describing cascade failure
propagation.
Dec 9, 2024
 The
application of nonequilibrium statistical physics in various other
branches of sciences, has been flourished in the past decades. The
modeling and tools of physics have opened a new way of analyzing
these complex system. Statistical physics can describe population
dynamics of animals or plants and can
explain extinction or oscillation phenomena observed in nature.
Besides the traditional mathematical approaches based on
differential equations it can take into account fluctuations
observed in predator-prey
models.
The
application of nonequilibrium statistical physics in various other
branches of sciences, has been flourished in the past decades. The
modeling and tools of physics have opened a new way of analyzing
these complex system. Statistical physics can describe population
dynamics of animals or plants and can
explain extinction or oscillation phenomena observed in nature.
Besides the traditional mathematical approaches based on
differential equations it can take into account fluctuations
observed in predator-prey
models. It
is worth to mention, that our model is closely related to a model
introduced by Drossel and Schwabl to investigate the effect of
immunization in an extension of the simple
forest-fire model.
That three-state model (0 is an empty site, 1 is a tree, and 2 is a
burning tree) differs
from our model in some details: the growth rate of a tree (s
: 0
->1) is p
, independently of
the environment, and a tree is ignited (s
: 1->
2) with rate (1-g
)Q
(n2
), (Q
is the usual
Heaviside function) .
This second process models the immunization of trees against fire.
The third process (s
: 2 ->
0) occurs at rate
1. For nonzero immunity and p>0, Albano showed that a transition
toward a single absorbing state is DP like, while for p=0 (at the
end point of the DP transition line), the transition belongs to the
dynamical percolation universality class, and the absorbing state is
not unique.
It
is worth to mention, that our model is closely related to a model
introduced by Drossel and Schwabl to investigate the effect of
immunization in an extension of the simple
forest-fire model.
That three-state model (0 is an empty site, 1 is a tree, and 2 is a
burning tree) differs
from our model in some details: the growth rate of a tree (s
: 0
->1) is p
, independently of
the environment, and a tree is ignited (s
: 1->
2) with rate (1-g
)Q
(n2
), (Q
is the usual
Heaviside function) .
This second process models the immunization of trees against fire.
The third process (s
: 2 ->
0) occurs at rate
1. For nonzero immunity and p>0, Albano showed that a transition
toward a single absorbing state is DP like, while for p=0 (at the
end point of the DP transition line), the transition belongs to the
dynamical percolation universality class, and the absorbing state is
not unique. The
The

